simoneb's blog

about design, development, profession and avoidance of fluff

Labeling Trees - Exercise 2

In the previous post of this series we did a small improvement to the state monad implementation by generalizing it over the type of the state. This is not exactly a requirement for labeling trees as the state can be simply an integer, but it’s a more natural choice now that we tackle the second exercise.

Go from labeling a tree to doing a constrained container computation, as in WPF. Give everything a bounding box, and size subtrees to fit inside their parents, recursively.

As you know the exercises come without any solution, so let’s try to understand what we need to do here. Because we’re talking about binary trees let’s assume that the requirement is to perform the constrained container computation based on containers with two children, where each child can either be another container or a terminal element, like a text block.

By translating it to WPF as suggested in the assignment we can represent a branch as a Grid with two rows and a single column. Each row’s unique cell can contain either another grid with the same characteristics or a TextBlock. The layout features of a grid match exactly the solution to the problem we’re asked to solve, as child elements of grid cells expand to match the size of their parent.

Starting with the same simple tree we used as a sample throughout the series:

A simple tree (a-simple-tree.cs) download
1
2
3
4
5
6
7
8
9
10

                                //  tree.Show() outputs:
var tree = branch(              //  Branch:
            leaf("a"),          //    Leaf: a
            branch(             //    Branch:
              branch(           //      Branch:
                leaf("b"),      //        Leaf: b
                leaf("c")),     //        Leaf: c
              leaf("d")));      //      Leaf: d

tree.Show();

we can transform it into this simple WPF markup, as described earlier:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

<Grid>
    <Grid.RowDefinitions>
        <RowDefinition></RowDefinition>
        <RowDefinition></RowDefinition>
    </Grid.RowDefinitions>
    <TextBlock Grid.Row="0">a</TextBlock>
    <Grid Grid.Row="1">
        <Grid.RowDefinitions>
            <RowDefinition></RowDefinition>
            <RowDefinition></RowDefinition>
        </Grid.RowDefinitions>
        <Grid Grid.Row="0">
            <Grid.RowDefinitions>
                <RowDefinition></RowDefinition>
                <RowDefinition></RowDefinition>
            </Grid.RowDefinitions>
            <TextBlock Grid.Row="0">b</TextBlock>
            <TextBlock Grid.Row="1">c</TextBlock>
        </Grid>
        <TextBlock Grid.Row="1">d</TextBlock>
    </Grid>
</Grid>

The result of this markup, along with some additional styling and a bit of logic to outline the bounds of each cell and display its box size, is shown below. The full code of this example is available as a ready-to-run LINQPad query here.

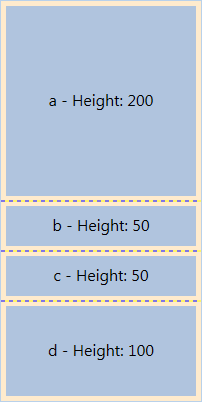
As you can see the children of grid cells automatically expand to fit their parent’s size. More precisely, each grid row gets 50% of the height of its parent, regardless of the contents. We’ll now try to do the same monadically by adapting our data structures and labeling logic to this new case.

First of all we need to decide what is the type of the state we’ll be carrying around. Intuitively, each time we branch a grid into its two rows we allocate 50% of the available height to each of them, therefore the state will certainly include the available height. Although not strictly needed in this scenario let’s make it a little more realistic by including the width as well, and we’ll call a structure containing two such values a Box. With this little piece of information we can already define the signature of our function which, similarly to the previous MLabel, will represent the entry point for the constrained box computation.

1

Tree<StateContent<Box, T>> MConstrainedBox<T>(Tree<T> tree, Box box)

The function takes a tree, which in this case we can imagine being a visual tree of graphic elements, and an initial box size (our initial state), representing the size of the root element. The return value is a tree whose generic argument is a tuple of state-content values. The state is the Box representing the size allocated to that tree and the value is the generic parameter T that we’re currently filling with characters to distinguish a leaf from another leaf.

As we did with the labeling problem the entry function will finally delegate to a helper function that will call itself recursively. We can thus define the body of the previous function as follows:

1
2
3
4

Tree<StateContent<Box, T>> MConstrainedBox<T>(Tree<T> tree, Box box)
{
    return MConstrainedBox1(tree).RunWithState(box).Item2;
}

No big surprises here as the juice is actually in the body of the MConstrainedBox1 function, in the same way as it previously was in MLabel1. Let’s start by defining its signature, which we can infer from above.

1

S<Box, Tree<StateContent<Box, T>>> MConstrainedBox1<T>(Tree<T> tree)

Not much else to do except reasoning about how to solve the problem of assigning box sizes to tree leaves according to the rules described earlier. The process is overall simple, let’s outline the steps.

If the current tree is a leaf then extract the state value using a proper getState function similar to what we used in the labeling scenario. The main difference here is that when we encounter leaves we do not need to update any state but only extract it from the monad and attach it to the new leaf we create.

If the current tree is a branch then:

  1. update the state by halving the height of the current box
  2. recurse over the left branch
  3. recurse over the right branch
  4. update the state by doubling the height of the current box
  5. return an instance of the state monad whose value is a branch with the results of steps 2 and 3 as the left and right trees, respectively

Let’s go through a simple example to understand better. Assuming to start with a box of size 200 x 400 (W x H) and that the root element of the tree we want to process is a branch, we halve the available height and process the left and right trees using 200 as the available height for each of them. If at some point we come across a leaf we use whatever current value of the state we have at that point during the computation (if both left and right trees are leaves then each of them will get a height of 200). When we’re done with the two trees we restore the original height by multiplying it by two. This leads exactly to the solution we’re looking for.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

public S<Box, Tree<StateContent<Box, T>>> MConstrainedBox1<T>(Tree<T> tree)
{
    if(tree is Leaf<T>)
    {
        var lf = tree as Leaf<T>;

        var getState = new S<Box, Box>
        {
            RunWithState = b0 => Tuple.Create(b0, b0)
        };

        return Bind(getState, b0 =>
                    Return<Box, Tree<StateContent<Box, T>>>(leaf(stateContent(b0, lf.Value))));
    }
    else
    {
        var br = tree as Branch<T>;

        var halveHeight = new S<Box, Box>
        {
            RunWithState = b0 => Tuple.Create(new Box(b0.Width, b0.Height/2), b0)
        };

        var doubleHeight = new S<Box, Box>
        {
            RunWithState = b0 => Tuple.Create(new Box(b0.Width, b0.Height*2), b0)
        };

        return Bind(halveHeight, _ => Bind(MConstrainedBox1(br.Left),
                    left => Bind(MConstrainedBox1(br.Right),
                    right => Bind(doubleHeight,  __ =>
                    Return<Box, Tree<StateContent<Box, T>>>(branch(left, right))))));
    }
}

Now if we run the computation against the same old tree:

1
2
3
4
5
6
7
8
9

var tree = branch(
               leaf("a"),
               branch(
                   branch(
                       leaf("b"),
                       leaf("c")),
                   leaf("d")));

MConstrainedBox(tree, new Box(200, 400)).Show();

the result we obtain is the same we obtained using WPF:

1
2
3
4
5
6
7

Branch:
  Leaf: { State = { Width = 200, Height = 200 }, Value = a }
  Branch:
    Branch:
      Leaf: { State = { Width = 200, Height = 50 }, Value = b }
      Leaf: { State = { Width = 200, Height = 50 }, Value = c }
    Leaf: { State = { Width = 200, Height = 100 }, Value = d }

The full source code is as usual available as a gist containing a LINQPad query that you can download an run right away. In the next post we’ll do a step forward in defining a self-contained monad type before moving on to more interesting and challenging exercises.

Comments